Matemática

FUNÇÃO POLINOMIAL

        Função de 1º Grau

Equações do tipo y = ax + b, sendo que  a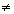0 e x a variável independente. Na função f(x) = ax + b, o número a é chamado de coeficiente de x e o número b é chamado termo constante.

 Veja alguns exemplos de funções polinomiais do 1º grau:

 f(x) = 5x - 3, onde a = 5 e b = - 3
 f(x) = -2x - 7, onde a = -2 e b = - 7
 f(x) = 11x, onde a = 11 e b = 0

Gráfico

    O gráfico de uma função polinomial do 1º grau,  y = ax + b, com a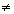0, é uma reta oblíqua aos eixos x e y.

Regra geral:

a função do 1º grau f(x) = ax + b é crescente quando o coeficiente de x é positivo (a > 0);
a função do 1º grau f(x) = ax + b é decrescente quando o coeficiente de x é negativo (a < 0)

Função de 2º Grau
Chama-se função quadrática, ou função polinomial do 2º grau, dada por uma lei da forma f(x) = ax² + bx + c, onde a, b e c são números reais e a 0.

Gráfico

    O gráfico de uma função polinomial do 2º grau, y = ax² + bx + c, com a 0, é uma curva chamada parábola.

Observação:

   Ao construir o gráfico de uma função quadrática y = ax² + bx + c, notaremos sempre que:

• se   a > 0, a parábola tem a concavidade voltada para cima;

• a > 0

  
  se   a < 0, a parábola tem a concavidade voltada para baixo;
  
  

  a < 0

  

Zero e Equação do 2º Grau

    Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax² + bx + c , a 0, os números reais x tais que f(x) = 0.

    Então as raízes da função f(x) = ax² + bx + c são as soluções da equação do 2º grau ax² + bx + c = 0, as quais são dadas pela chamada fórmula de Bhaskara:

Trigonometria no triângulo Retângulo

O triângulo é a figura mais simples e uma das mais importantes da Geometria, ele é objeto de estudos desde os povos antigos. O triângulo possui propriedades e definições de acordo com o tamanho de seus lados e medida dos ângulos internos. Quanto aos lados, o triângulo pode ser classificado da seguinte forma: 

Equilátero: possui os lados com medidas iguais. 
Isósceles: possui dois lados com medidas iguais. 
Escaleno: possui todos os lados com medidas diferentes. 

Quanto aos ângulos, os triângulos podem ser denominados:

Acutângulo: possui os ângulos internos com medidas menores que 90º 
Obtusângulo: possui um dos ângulos com medida maior que 90º. 
Retângulo: possui um ângulo com medida de 90º, chamado ângulo reto.

No triângulo retângulo existem algumas importantes relações, uma delas é o Teorema de Pitágoras, que diz o seguinte: “A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa”. Essa relação é muito importante na geometria, atende inúmeras situações envolvendo medidas.

As relações trigonométricas existentes no triângulo retângulo admitem três casos: seno, cosseno e tangente.


Vamos determinar as relações de acordo com o triângulo BAC com lados medindo a, b e c.

senoB = b/a
cossenoB = c/a
tangenteB = b/c

senoC = c/a
cossenoC = b/a
tangenteC = c/b 


A trigonometria possui diversas aplicações no cotidiano, abrange áreas relacionadas à Astronomia, Física, Geometria, Navegação entre outras.






Recuperação de Matemática (1a etapa):
Semelhança:
-Figuras semelhantes


Duas figuras são SEMELHANTES, quando de uma para a outra:
● os ângulos correspondentes são geometricamente iguais e,
● os comprimentos dos lados correspondentes são diretamente proporcionais.


-Razão de semelhança

●A razão de semelhança de dois polígonos é igual à razão entre os comprimentos dos
lados correspondentes.


-Relações métricas no Triângulo retângulo
Observe os triângulos:


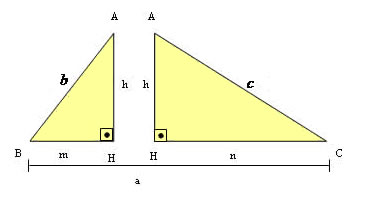
Os triângulos AHB e AHC são semelhantes, então podemos estabelecer algumas relações métricas importantes:


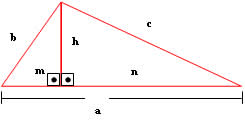
h² = mn           b² = ma               c² = an              bc = ah

-Teorema De Pitágoras:

Catetos: a e b
Hipotenusa: c

O Teorema diz que: “a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.”

a² + b² = c²

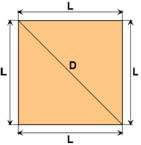
Diagonal do quadrado

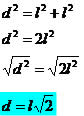
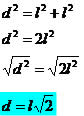
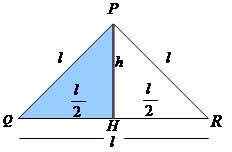
Altura de um triângulo equilátero




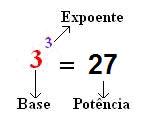
-POTÊNCIAS E RAÍZES
-A potenciação é uma operação que consiste em multiplicar uma BASE tantas vezes que indicar seu EXPOENTE
2 . 2 . 2 . 2 = 16 → multiplicação de fatores iguais. 

Podemos representar a mesma multiplicação da seguinte forma: 

2 . 2 . 2 . 2 = 2⁴ = 16 
           ↓ 
Fatores iguais. 







                                 

Número inteiro no expoente



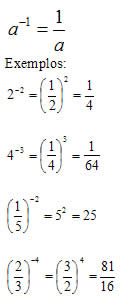
Propriedades da potenciação

Multiplicação de potências de mesma base: “conservar a base e somar os expoentes”.


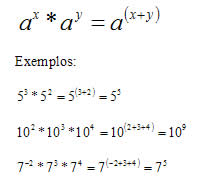
Divisão de potências de mesma base: “conservar a base e subtrair os expoentes”.


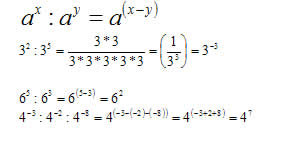
Potência de potência



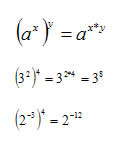
Multiplicação de potências de mesmo expoente: “conservar os expoentes e multiplicar as bases”.



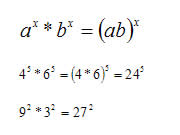
Divisão de potências de mesmo expoente: “conservar os expoentes e dividir as bases”.


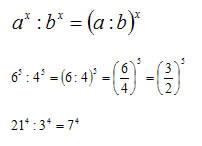
Frações Algébricas e numéricas
 

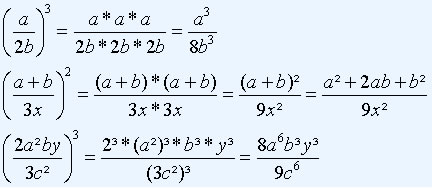
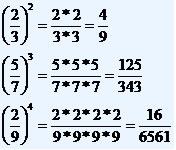
Potências de expoente fracionário:



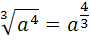
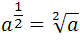
Uma potência de expoente fracionário pode ser transformada em uma raiz, onde o índice é o denominador do expoente fracionário e o radicando é a base da potência elevada ai numerador do expoente

-NOTAÇÃO CIENTÍFICA
A forma de uma Notação científica é: m . 10 ^e, onde m significa mantissa e E significa ordem de grandeza. A mantissa SEMPRE será um valor em módulo entre 1 e 10.

Para transformar um numero grande qualquer em notação cientifica, devemos deslocar a vírgula para a esquerda até o primeiro algarismo desta forma:

200 000 000 000 » 2,00 000 000 000

note que a vírgula avançou 11 casas para a esquerda, entao em notação cientifica este numero fica: 

2 . 10¹¹.

Para com valores muito pequenos, é só mover a virgula para a direita, e a cada casa avançada, diminuir 1 da ordem de grandeza:

0,0000000586 » movendo a virgula para direita » 5,86 (avanço de 8 casas) » 5,86 . 10^-8

-12.000.000.000.000 » -1,2 . 10¹³

^{-SIMPLIFICAÇÃO DE RADICAIS}

 

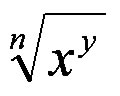
n: índice da raiz 

a: radicando
b: raiz 

1º propriedade: O expoente do radicando é menor que o índice. Dessa forma, reduzimos o índice e o expoente através da utilização do máximo divisor comum aos termos

2ª propriedade: O expoente do radicando é maior ou igual ao índice. Dessa forma, simplificamos o expoente pelo mesmo valor do índice e retiramos a base do radicando

3ª propriedade: Introdução de termos no radicando. O termo externo introduzido no radicando, recebe como expoente o mesmo valor numérico do índice.

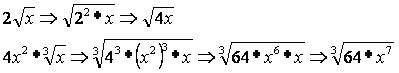
4ª propriedade: Simplificação de radicais com frações algébricas no radicando.

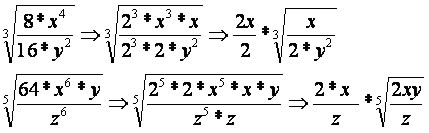
5ª propriedade: Raiz de números na forma de fração. Nesse caso, devemos extrair a raiz do numerador e do denominador da fração numérica, fornecendo o resultado na forma de fração.

6ª propriedade: Racionalização de denominadores. Pode ocorrer em algumas frações, a presença de radicais no denominador. Caso a raiz do radical envolva como resultado, números irracionais, o cálculo se torna complexo. Por isso, devemos racionalizar as frações com radicais no denominador. A racionalização é feita multiplicando os membros da fração pelo radical presente no denominador.

Galera, a matéria que segue no roteiro já foi postada no blog, anteriormente, então não irei escreve-las aqui (e também estou meio sem tempo, me desculpem) Mas, da próxima, passo o resumo de todo o roteiro de recuperação, se pedirem.

Prova 11/06

COLÉGIO MAGNUM AGOSTINIANO

Roteiro de estudo da prova dia 11/06

Matemática – 2ª prova – 2ª etapa

Prof. Paulo Roberto Silva

2ª prova – prova aberta – 7,0 pontos

Data: 11 / 06 / 2012

CONTEÚDO:            - Sistema Métrico Decimal

- Transformação de unidades de medidas

- Medidas de comprimento

- Medidas de área

- Problema envolvendo cálculo de área de figuras planas

- Medidas de volume

- Problema envolvendo cálculo de volume de figuras sólidas

- Medidas de capacidade

- Medidas de massa

-Cálculo de porcentagem

- Problema envolvendo porcentagem

HABILIDADES EXIGIDAS:

- Transformar unidades de medidas do Sistema Métrico Decimal

- Resolver situação problema envolvendo cálculo de áreas de figuras planas convencionais.

- Resolver situação problema envolvendo cálculo de volume de sólidos convencionais e não convencionais.

- Converter medida de volume em medida de capacidade

- Efetuar cálculo de porcentagem usando números decimais ou regras de três

- Resolver situação problema envolvendo cálculo de porcentagem

ONDE ESTUDAR:

- O conteúdo de Medidas é trabalhado no capítulo 4 do livro-texto, porém os exercícios realizados são do bloco de exercícios da 1ª etapa – nº 94 a 119 – o bloco de exercícios da 1ª etapa está disponível no Magnum-Sol.

- O conteúdo de Porcentagem é trabalhado no início do capítulo 8 do livro-texto. Os exercícios nº 1 a 12 do livro referem-se ao conteúdo de porcentagem. Problemas envolvendo porcentagem serão cobrados na prova, mas problemas com regras de três compostas e juros simples não serão cobrados na prova. Os exercícios do bloco da 2ª etapa referentes ao conteúdo de porcentagem são os de nº 40, 43, 48, 49, 50, 58, 59, 60, 61, 63, 65, 66.

            Caro (a) aluno (a), refaça os exercícios dos blocos que são sugeridos nesse roteiro. Trabalhe bastante, efetuando os cálculos com muita atenção. Treine bastante, sempre tentando compreender. 

Um abraço, bons estudos, Paulo Roberto. 

1 - Medidas de comprimento  

No sistema métrico decimal, a unidade fundamental para medir comprimentos é o metro, cuja abreviação ém. Existem os múltiplos e os submúltiplos do metro, veja na tabela: 

Múltiplos				u.f.	Submúltiplos
quilômetro	hectômetro	decâmetro	metro		Decímetro	centímetro	Milímetro
km	hm	dam	m		Dm	cm	mm
1 000 m	100 m	10 m	1 m		0,1 m	0,01 m	0,001 m

Existem outras unidades de medida mas que não pertencem ao sistema métrico decimal. Vejamos as relações entre algumas dessas unidades e as do sistema métrico decimal:

1 polegada = 25 milímetros
1 milha      = 1 609 metros
1 légua      = 5 555 metros
1 pé          = 30 centímetros

Obs: valores aprximados

1.1 - Transformação de unidades de comprimento 

Observando o quadro das unidades de comprimento, podemos dizer que cada unidade de comprimento é 10 vezes maior que a unidade imediatamente inferior, isto é, as sucessivas unidades variam de 10 em 10. Concluí-se então que para transformar uma unidade para um submúltiplo, basta multiplicar por 10ⁿ  onde n é o número de colunas à direita do número na tabela. Já para passar para um múltiplo, basta dividir por 10ⁿ  onde n é o número de colunas à esquerda do número na tabela. 

Por exemplo: 7 m = 7 x 10² cm = 700 cm

                       500 m = 500 x 10^-3 km = 0,5 km

2- Medidas de área 

No sistema métrico decimal, a unidade fundamental para medir área é o metro quadrado, cuja representação é m² . O metro quadrado é a medida da superfície de um quadrado de um metro de lado. Como na medida de comprimento, na área também temos os múltiplos e os submúltiplos:

Múltiplos				u.f.	Submúltiplos
km2	hm2	dam2	m2		dm2	cm2	mm2
1 000 000 m2	10 000 m2	100 m2	1 m2		0,01 m2	0,0001 m2	0,000001 m2

2.1 - Transformação de unidades de área

Analogamente à transformação de unidades da medida de comprimento, faremos para a medida de área, porém para cada devemos multiplicar ou dividir por 10² e não 10. Veja os exemplos: 

a)      5 m² = 5 x 10² dm² = 500 dm²

b)      3 km² = 3 x 10⁶ m² = 3 000 000 m²

c)      20 000 m² = 20 000 x 10^-6 km² = 0,02 km²

obs. Quando queremos medir grandes porções de terra (como sítios, fazendas etc.) usamos uma unidade agrária chamada hectare (ha).

O hectare é a medida de superfície de um quadrado de 100 m de lado. 

1 hectare (há) = 1 hm² = 10 000 m² 

Em alguns estados do Brasil, utiliza-se também uma unidade não legal chamada alqueire. 

- 1 alqueire mineiro é equivalente a 48 400 m².

- 1 alqueire paulista é equivalente a 24 200 m².

3 - Áreas das figuras geométricas planas 

Constantemente no estudo de gráficos, precisamos determinar a área compreendida entre a curva e o eixo-x. Daremos aqui as fórmulas, para o cálculo da área, das figuras mais utilizadas na Física.  

Imagine a seguinte situação:

Aproveitando uma promoção de uma loja de materiais para construção, uma família resolve trocar o piso da sala de sua residência. Sabem que a sala mede 4 metros de largura e possui um comprimento de 5,5 metros. Sabem também que o ladrilho desejado é quadrado, com 25 cm de lado. Quantos ladrilhos serão necessários para ladrilhar o piso da sala inteira?

Área é a denominação dada à medida de uma superfície. Na situação acima estamos nos referindo às áreas da sala e do ladrilho.

Partindo-se deste princípio, o nosso problema se resume ao cálculo da razão entre as áreas da sala e do ladrilho.

Para que você saiba solucionar, dentre outros, o problema acima, vamos então nos atentar ao método de cálculo da área das figuras geométricas planas mais comuns.

De qualquer forma, no final da página você encontra a resolução detalhada do problema acima.

Cálculo da Área do Triângulo

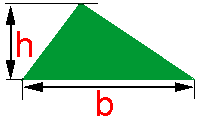
Denominamos de triângulo a um polígono de três lados.

Observe a figura ao lado. A letra h representa a medida da altura do triângulo, assim como letra b representa a medida da sua base.

A área do triângulo será metade do produto do valor da medida da base, pelo valor da medida da altura, tal como na fórmula abaixo:

A letra S representa a área ou superfície do triângulo.

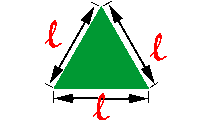
No caso do triângulo equilátero, que possui os três ângulos internos iguais, assim como os seus três lados, podemos utilizar a seguinte fórmula:

Onde l representa a medida dos lados do triângulo.

Exemplos

A medida da base de um triângulo é de 7 cm, visto que a medida da sua altura é de 3,5 cm, qual é a área deste triângulo?

Do enunciado temos:

Utilizando a fórmula:

A área deste triângulo é 12,25 cm².

Os lados de um triângulo equilátero medem 5 mm. Qual é a área deste triângulo equilátero?

Segundo o enunciado temos:

Substituindo na fórmula:

A área deste triângulo equilátero é de aproximadamente 10,8 mm².

Cálculo da Área do Paralelogramo

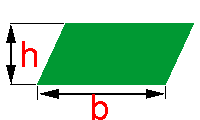
Um quadrilátero cujos lados opostos são iguais e paralelos é denominadoparalelogramo.

Com h representando a medida da sua altura e com b representando a medida da sua base, a área do paralelogramo pode ser obtida multiplicando-se b por h, tal como na fórmula abaixo:

Exemplos

A medida da base de um paralelogramo é de 5,2 dm, sendo que a medida da altura é de 1,5 dm. Qual é a área deste polígono?

Segundo o enunciado temos:

Substituindo na fórmula:

A área deste polígono é 7,8 dm².

Qual é a medida da área de um paralelogramo cujas medidas da altura e da base são respectivamente 10 cm e 2 dm?

Sabemos que 2 dm equivalem a 20 cm, temos:

Substituindo na fórmula:

A medida da área deste paralelogramo é 200 cm² ou 2 dm².

 

Cálculo da Área do Losango

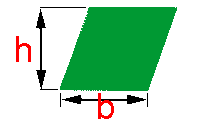
O losango é um tipo particular de paralelogramo. Neste caso além dos lados opostos serem paralelos, todos os quatro lados são iguais.

Se você dispuser do valor das medidas h e b, você poderá utilizar a fórmula do paralelogramo para obter a área do losango.

Outra característica do losango é que as suas diagonais são perpendiculares.

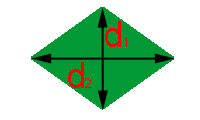
Observe na figura à direita, que a partir das diagonais podemos dividir o losango em quatro triângulos iguais.

Consideremos a base b como a metade da diagonal d₁ e a altura h como a metade da diagonal d₂, para calcularmos a área de um destes quatro triângulos. Bastará então que a multipliquemos por 4, para obtermos a área do losango. Vejamos:

Realizando as devidas simplificações chegaremos à fórmula:

Exemplos

As diagonais de um losango medem 10 cm e 15 cm. Qual é a medida da sua superfície?

Para o cálculo da superfície utilizaremos a fórmula que envolve as diagonais, cujos valores temos abaixo:

Utilizando na fórmula temos:

A medida da superfície deste losango é de 75 cm²

Qual é a medida da área de um losango cuja base mede 12 cm e cuja altura seja de 9 cm?

Neste caso, para o cálculo da área utilizaremos a fórmula do paralelogramo, onde utilizamos a base e a altura da figura geométrica, cujos valores temos abaixo:

Segundo a fórmula temos:

A medida da área do losango é de 108 cm².

Cálculo da Área do Quadrado

Todo quadrado é também um losango, mas nem todo losango vem a ser um quadrado, do mesmo modo que todo quadrado é um retângulo, mas nem todo retângulo é um quadrado.

O quadrado é um losango, que além de possuir quatro lados iguais, com diagonais perpendiculares, ainda possui todos os seus ângulos internos iguais a 90°. Observe ainda que além de perpendiculares, as diagonais também são iguais.

Por ser o quadrado um losango e por ser o losango um paralelogramo, podemos utilizar para o cálculo da área do quadrado, as mesmas fórmulas utilizadas para o cálculo da área tanto do losango, quanto do paralelogramo.

Quando dispomos da medida do lado do quadrado, podemos utilizar a fórmula do paralelogramo:

Como h e b possuem a mesma medida, podemos substituí-las por l, ficando a fórmula então como sendo:

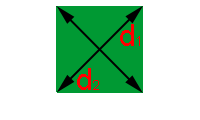
Quando dispomos da medida das diagonais do quadrado, podemos utilizar a fórmula do losango:

Como ambas as diagonais são idênticas, podemos substituí-las por d, simplificando a fórmula para:

Exemplos

A lateral da tampa quadrada de uma caixa mede 17 cm. Qual a superfície desta tampa?

Do enunciado temos que a variável l é igual a 17:

Substituindo na fórmula temos:

Portanto a superfície da tampa desta caixa é de 289 cm².

A medida do lado de um quadrado é de 20 cm. Qual é a sua área?

Como o lado mede 20 cm, temos:

Substituindo na fórmula temos:

A área do quadrado é de 400 cm².

A área de um quadrado é igual a 196 cm². Qual a medida do lado deste quadrado?

Temos que S é igual a 196.

Utilizando a fórmula temos:

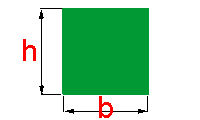
Como a medida do lado não pode ser negativa, temos que o lado do quadrado mede 14 cm.

Cálculo da Área do Retângulo

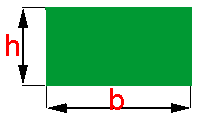
Por definição o retângulo é um quadrilátero equiângulo (todo os seus ângulos internos são iguais), cujos lados opostos são iguais.

Se todos os seus quatro lados forem iguais, teremos um tipo especial de retângulo, chamado de quadrado.

Por ser o retângulo um paralelogramo, o cálculo da sua área é realizado da mesma forma.

Se denominarmos as medidas dos lados de um retângulo como na figura ao lado, teremos a seguinte fórmula:

Exemplos

Um terreno mede 5 metros de largura por 25 metros de comprimento. Qual é a área deste terreno?

Atribuindo 5 à variável h e 25 à variável b temos:

Utilizando a fórmula:

A área deste terreno é de 125 m².

A tampa de uma caixa de sapatos tem as dimensões 30 cm por 15 cm. Qual a área desta tampa?

Podemos atribuir 15 à variável h e 30 à variável b:

Ao substituirmos as variáveis na fórmula teremos:

Portanto a área da tampa da caixa de sapatos é de 450 cm².

 

Resolução Detalhada do Problema no Começo da Página

Para resolvermos tal problema, primeiramente vamos calcular a área da sala.

Para podermos utilizar a fórmula do cálculo da área de um retângulo, vamos atribuir os 4 m da largura à letra h e os 5,5 m do comprimento à letra b:

Resolvendo através da fórmula:

Agora que sabemos que a sala tem uma área de 22 m², precisamos conhecer a área do ladrilho.

Como o ladrilho é quadrado, precisamos calcular a área de um quadrado, só que devemos trabalhar em metros e não em centímetros, pois a área da sala foi calculada utilizando-se medidas em metros e não medidas emcentímetros. Poderíamos ter convertido as medidas da sala em centímetros, para trabalharmos apenas comcentímetros. O importante é que utilizemos sempre a mesma unidade (múltiplo/submúltiplo).

A transformação de 25 cm em metros é realizada dividindo-se tal medida por 100:

Então a medida dos lados dos ladrilhos é de 0,25 m.

Se tiver dúvidas sobre como realizar tal conversão, por favor acesse a página que trata sobre as unidades de medidas, lá você encontrará várias informações sobre este assunto, incluindo vários exemplos e um link para umacalculadora sobre o tema.

Voltando ao problema, como o ladrilho é quadrado, a área do ladrilho com lado l = 0,25 é igual a:

Como dito no começo da página, a resolução do problema se resume ao cálculo da razão entre a área da sala e a área do ladrilho.

Como a sala tem uma área de 22 m² e o ladrilho de 0,0625 m², temos a seguinte razão:

Ou seja, para ladrilhar o piso da sala inteira serão necessários ladrilhos 352.

4 - Medidas de volume

No sistema métrico decimal, a unidade fundamental para medir volume é o metro cúbico, cuja abreviatura ém³ . O metro cúbico (m³) é o volume ocupado por um cubo de 1 m  de aresta. Como nas medidas de comprimento e de área, no volume também temos os múltiplos e os submúltiplos: 

Múltiplos				u.f.	Submúltiplos
km3	hm3	dam3	m3		dm3	cm3	mm3
1 000 000 000 m3	1000 000 m3	1000 m3	1 m3		0,001 m3	0,00001 m3	0,000000001 m3

As mais utilizadas, além do metro cúbico, são o decímetro cúbico e o centímetro cúbico.

4.1 - Transformação de unidades de volume

Analogamente à transformação de unidades da medida de comprimento, faremos para a medida de área, porém para cada devemos multiplicar ou dividir por 10³ e não 10. Veja os exemplos:   

a) 8,2 m³ = 8,2 x 103 dm³ = 8 200 dm³

b) 500 000 cm³ = 500 000 x 10^-6 m³ = 0,5 m³

Calculando volumes de Sólidos geométricos

Exercício 1: (FUVEST 2009)

Os papiros mostram que os egípcios antigos possuíam diversos conhecimentos matemáticos. Eles sabiam que o volume da pirâmide equivale a um terço do volume do prisma que a contém. A maior pirâmide egípcia, Quéops, construída por volta de 2560 a.C., tem uma altura aproximada de 140 metros e sua base é um quadrado com lados medindo aproximadamente 230 metros. Logo, o volume da pirâmide de Quéops é de aproximadamente (em milhões de metros cúbicos):

A)	1,2
B)	2,5
C)	5
D)	7,5
E)	15

---

Exercício 2: (UDESC 2010)

A planificação da superfície lateral de um cilindro circular reto de altura h e raio r gera a região retangular ABCD, conforme é ilustrado na Figura 1. Suponha que esta região seja utilizada para construir um novo cilindro, cuja altura é a medida do segmento AB , sem haver sobreposição.

O volume do novo cilindro é:

A)
B)
C)
D)
E)

---

Exercício 3: (UDESC 2009)

Um cilindro circular reto e um cone reto possuem a mesma altura h e o mesmo raio r da base. Uma semi-esfera é retirada do interior do cilindro e é acrescentada no topo do cone, gerando os sólidos S₁ e S₂ , conforme mostra a figura.

Se os volumes desses sólidos são representados, respectivamente, por Vol(S1) e Vol(S2) , é correto afirmar que:

A)	Vol (S1) = Vol (S2) se e somente se h = 2r .
B)	Vol (S1) = Vol (S2) se e somente se r = 2h
C)	Vol (S1) = Vol (S2) para quaisquer valores de r e h.
D)	Vol (S1) > Vol (S2) para quaisquer valores de r e h.
E)	Vol (S1) < Vol (S2) para quaisquer valores de r e h.

---

Exercício 4: (UFMG 2008)

Considere um reservatório, em forma de paralelepípedo retângulo, cujas medidas são 8 m de comprimento, 5 m de largura e 120 cm de profundidade. Bombeia-se água para dentro desse reservatório, inicialmente vazio, a uma taxa de 2 litros por segundo. Com base nessas informações, é CORRETO afirmar que, para se encher completamente esse reservatório, serão necessários:

A)	40 min .
B)	240 min .
C)	400 min .
D)	480 min .

---

Exercício 5: (ADVISE 2009)

Se aumentarmos em 20% (vinte por cento) as arestas de um paralelepípedo retângulo, em quantos por cento o seu volume será aumentado:

A)	20%
B)	33,1%
C)	60%
D)	72,8%
E)	80%

---

Exercício 6: (UDESC 2008)

O volume do prisma reto de altura h = 2 cm, cuja base é o quadrilátero de vértices A(1, 2) , B(2, 3) , C(0, 6) e D(5, 2) , é:

A)	57 cm³
B)	72 cm ³
C)	26 cm ³
D)	24 cm ³
E)	36 cm ³

5 - Medidas de capacidade

A unidade fundamental para medir capacidade de um sólido é o litro.

De acordo com o Comitê Internacional de Pesos e Medidas, o litro é, aproximadamente, o volume equivalente a um decímetro cúbico, ou seja:

1 litro = 1,000027 dm³ 

Porém, para todas as aplicações práticas, simples, podemos definir:

1 litro = 1 dm³

Veja os exemplos: 

1) Na leitura do hidrômetro de uma casa, verificou-se que o consumo do último mês foi de 36 m³. Quantos litros de água foram consumidos?  

Solução: 36 m³ = 36 000 dm³  =  36 000 litros

2) Uma indústria farmacêutica fabrica 1 400 litros de uma vacina que devem ser colocados em ampolas de 35 cm³ cada uma. Quantas ampolas serão obtidas com essa quantidade de vacina?  

Solução: 1 400 litros = 1 400 dm³ = 1 400 000 cm³
                 (1 400 000 cm³) : (35 cm³) = 40 000 ampolas.

5.1 - Outras unidades para medir a capacidade 

São também utilizadas outras unidades para medir capacidade, que são múltiplos e submúltiplos do litro: 

Múltiplos			u.f.	Submúltiplos
hectolitro	decalitro	litro		decilitro	centilitro	mililitro
hl	dal	l		dl	cl	ml
100 l	10 l	1 l		0,1 l	0,01 l	0,001 l

Obs. 1) Não é usado nem consta da lei o quilolitro.  

Obs. 2) Além do litro, a unidade mais usado é o mililitro (ml), principalmente para medir pequenos volumes, como a quantidade de líquido de uma garrafa, de uma lata ou de uma ampola de injeção.

5.1.1 - Transformação de unidades de capacidade

Observando o quadro das unidades de capacidade, podemos verificar que cada unidade de capacidade é 10 vezes maior que a unidade imediatamente inferior, isto é, as sucessivas unidades variam de 10 em 10.

Veja os exemplos: 

1) Expressar 15 l em ml.   

Solução:  15 l = (15 x 10³) ml  =  15 000 ml  

2) Expressar 250 ml em cm³.  

Solução: 250 ml = 0,25 l = 0,25 dm³ = 250 cm³

A Unidade de Massa

Dentro de nosso sistema métrico decimal, consideramos como unidade fundamental de massa o quilograma ( kg ) . Para mantermos a coerência com as demais medidas, ainda consideraremos o grama ( g ) como unidade fundamental.

A Diferença entre Peso e Massa

Definimos Massa como sendo a quantidade de matéria presente em um corpo e efinimos peso como sendo a ação da força da gravidade sobre essa massa. Como a força da gravidade varia de acordo com a distância que o objeto se encontra do centro da terra,

o peso é variável, mas a massa de um corpo é sempre constante. Numa mesma região os conceitos de massa e peso podem ser considerados iguais.

Outras Unidades de Massa

Além do grama e do quilograma, utilizamos outras unidades para medir a massa dos corpos. São elas :

Múltiplos do grama  

decagrama ( dag ) - Capacidade equivalente a 10 gramas  1 dag  = 10 g

hectograma ( hg ) - Capacidade equivalente a 100 gramas    1 hg  = 100 g

tonelada ( t) - Capacidade equivalente a 1 000 quilogramas    1 t  = 1 000 kg

Submúltiplos do grama  

decigrama ( dg ) - Capacidade equivalente a 0,1 gramas     1 dg  = 0,1 g  1 g = 10 dg

centigrama ( cg ) - Capacidade equivalente a 0,01 gramas   1 cg  = 0,01 g  1 g = 100 cg

miligrama ( mg ) - Capacidade equivalente a 0,001 gramas   1 mg  = 0,001 g  1 g = 1.000 mg

E montando uma tabela, teremos :

Múltiplos do grama				Unidade Fundamental	Submúltiplos da grama
tonelada	quilograma	hectograma	decagrama	grama	decigrama	centigrama	miligrama
t	kg	hg	dag	g	dg	cg	mg
1 000 kg	1 000 g	100 g	10 g	1 g	0,1 g	0,01 g	0,001 g

Transformação de Unidades de Massa

Exatamente como acontece com as unidades de capacidade, as unidades de massa variam como as unidades de comprimento, ou seja:

Cada unidade é 10 vezes maior que a unidade que a antecede. A grande exceção é a tonelada que é equivalente a 1 000 kg. Assim :

O grama é 10 vezes maior que o decigrama, 100 vezes maior que o centigrama e 1 000 vezes maior que o miligrama.

O grama é 10 vezes menor que o decagrama, 100 vezes menor que o hectograma e 1 000 vezes menor que o quilograma e um milhão de vezes menor que a tonelada

Exemplo 12: Transfomar 7,61 hg para cg

De 7,61 hg para dg caminharemos três casas para a direita, com isso, andaremos com a vírgula para a direita três casas,

Assim: 7,61 hg = 7. 610 dg

Exemplo 13: Transfomar 82.509 cg para kg

De 82.509 cg para kg caminharemos cinco casas para a esquerda, com isso, andaremos com a vírgula cinco casas para a esquerda, 

Assim: 82.509 cg = 0,825 09 kg

Exemplo 14: Transfomar 0,045 t para dag

0,045 t para dag caminharemos três casas para a direita para transformarmos tonelada em quilograma e andaremos mais duas casas para chegarmos a decagrama, com isso, andaremos com a vírgula cinco casas para a direita, 

Assim: 0,045 t = 4.500 dag

Exemplos de Conversão entre Unidades de Medida

Converta 2,5 metros em centímetros

Para convertermos 2,5 metros em centímetros, devemos multiplicar (porque na tabela metro está à esquerda decentímetro) 2,5 por 10 duas vezes, pois para passarmos de metros para centímetros saltamos dois níveis à direita. Primeiro passamos de metros para decímetros e depois de decímetros para centímetros:

Isto equivale a passar a vírgula duas casas para a direita.

Portanto:

2,5 m é igual a 250 cm

Passe 5.200 gramas para quilogramas

Para passarmos 5.200 gramas para quilogramas, devemos dividir (porque na tabela grama está à direita dequilograma) 5.200 por 10 três vezes, pois para passarmos de gramas para quilogramas saltamos três níveis à esquerda. Primeiro passamos de grama para decagrama, depois de decagrama para hectograma e finalmente dehectograma para quilograma:

Isto equivale a passar a vírgula três casas para a esquerda.

Portanto:

5.200 g é igual a 5,2 kg

Quantos centilitros equivalem a 15 hl?

Para irmos de hectolitros a centilitros, passaremos quatro níveis à direita. Multiplicaremos então 15 por 10 quatro vezes:

Isto equivale a passar a vírgula quatro casas para a direita.

Portanto:

150.000 cl equivalem a 15 hl.

Quantos quilômetros cúbicos equivalem a 14 mm³?

Para passarmos de milímetros cúbicos para quilômetros cúbicos, passaremos seis níveis à esquerda. Dividiremos então 14 por 1000 seis vezes:

Portanto:

0,000000000000000014 km³, ou a 1,4 x 10^-17 km³ se expresso em notação científica equivalem a 14 mm³.

Passe 50 dm² para hectometros quadrados

Para passarmos de decímetros quadrados para hectometros quadrados, passaremos três níveis à esquerda. Dividiremos então por 100 três vezes:

Isto equivale a passar a vírgula seis casas para a esquerda.

Portanto:

50 dm² é igual a 0,00005 hm²

Equivalência entre medidas de volume e medidas de capacidade

Um cubo com aresta de 10 cm terá um volume de 1.000 cm³, medida esta equivalente a 1 l.

Como 1.000 cm³ equivalem a 1 dm³, temos que 1 dm³ equivale a 1 l.

Como um litro equivale a 1.000 ml, podemos afirmar que 1 cm³ equivale a 1 ml.

1.000 dm³ equivalem a 1 m³, portanto 1 m³ é equivalente a 1.000 l, que equivalem a 1 kl.

Exemplos de Conversão entre Medidas de Volume e Medidas de Capacidade

Quantos decalitros equivalem a 1 m³?

Sabemos que 1 m³ equivale a 1.000 l, portanto para convertermos de litros a decalitros, passaremos um nível à esquerda. Dividiremos então 1.000 por 10 apenas uma vez:

Isto equivale a passar a vírgula uma casa para a esquerda.

Poderíamos também raciocinar da seguinte forma:

Como 1 m³ equivale a 1 kl, basta fazermos a conversão de 1 kl para decalitros, quando então passaremos dois níveis à direita. Multiplicaremos então 1 por 10 duas vezes:

Portanto:

100 dal equivalem a 1 m³.

348 mm³ equivalem a quantos decilitros?

Como 1 cm³ equivale a 1 ml, é melhor dividirmos 348 mm³ por mil, para obtermos o seu equivalente em centimetros cúbicos: 0,348 cm³. Logo 348 mm³ equivale a 0,348 ml, já que cm³ e ml se equivalem.

Neste ponto já convertemos de uma unidade de medida de volume, para uma unidade de medida de capacidade.

Falta-nos passarmos de mililitros para decilitros, quando então passaremos dois níveis à esquerda. Dividiremos então por 10 duas vezes:

Logo:

348 mm³ equivalem a 0,00348 dl.

PORCENTAGEM

    É frequente o uso de expressões que refletem acréscimos ou reduções em preços, números ou quantidades, sempre tomando por base 100 unidades. Alguns exemplos:

• A gasolina teve um aumento de 15%
  Significa que em cada R$100 houve um acréscimo de R$15,00
• O cliente recebeu um desconto de 10% em todas as mercadorias.
  Significa que em cada R$100 foi dado um desconto de R$10,00
• Dos jogadores que jogam no Grêmio, 90% são craques.
  Significa que em cada 100 jogadores que jogam no Grêmio, 90 são craques.
     

    Razão centesimal 

    Toda a razão que tem para consequente o número 100 denomina-se razão centesimal. Alguns exemplos:

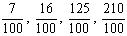
    Podemos representar uma razão centesimal de outras formas:

    

    As expressões 7%, 16% e 125% são chamadas taxas centesimais ou taxas percentuais.

    Considere o seguinte problema:

    João vendeu 50% dos seus 50 cavalos. Quantos cavalos ele vendeu?    Para solucionar esse problema devemos aplicar a taxa percentual (50%) sobre o total de cavalos.

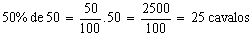
    Logo, ele vendeu 25 cavalos, que representa a porcentagem procurada.

    Portanto, chegamos a seguinte definição:

Porcentagem é o valor obtido ao aplicarmos uma taxa percentual a um determinado valor.

    Exemplos:

• Calcular 10% de 300.        
     
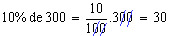
• Calcular 25% de 200kg.
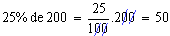          Logo, 50kg é o valor correspondente à porcentagem procurada.
  

   

---

    Uma dica importante: o FATOR DE MULTIPLICAÇÃO.

    Se, por exemplo, há um acréscimo de 10% a um determinado valor, podemos calcular o novo valor apenas multiplicando esse valor por 1,10, que é o fator de multiplicação. Se o acréscimo for de 20%, multiplicamos por 1,20, e assim por diante. Veja a tabela abaixo:

Acréscimo ou Lucro	Fator de Multiplicação
10%	1,10
15%	1,15
20%	1,20
47%	1,47
67%	1,67

    Exemplo: Aumentando 10% no valor de R$10,00 temos: 10 * 1,10 = R$ 11,00

    No caso de haver um decréscimo, o fator de multiplicação será:
    Fator de Multiplicação =  1 - taxa de desconto (na forma decimal)

    Veja a tabela abaixo:

Desconto	Fator de Multiplicação
10%	0,90
25%	0,75
34%	0,66
60%	0,40
90%	0,10

    Exemplo: Descontando 10% no valor de R$10,00 temos: 10 * 0,90 = R$ 9,00

Exercícios:

• 1) Quanto é 15% de 80?
•  
• 2) Quanto é 70% de 30?
•  
• 3) Quanto é 150% de 45?
•  
• 4) Quanto é 100% de 40?
•  
• 5) Expresse a razão de 19 para 25 como uma porcentagem.
•  
• 6) 30% da população de uma cidade litorânea mora na área insular e os demais 337.799 habitantes moram na área continental. Quantas pessoas moram na ilha?
•  
• 7) Se 4% de um número é igual a 15, quanto é 20% deste número?
•  
• 8) Do meu salário R$ 1.200,00 tive um desconto total de R$ 240,00. Este desconto equivale a quantos por cento do meu salário?
•  
• 9) Eu tenho 20 anos. Meu irmão tem 12 anos. A idade dele é quantos por cento da minha?
•  
• 10) Meu carro alcança uma velocidade máxima de 160 km/h. O carro de meu pai atinge até 200 km/h. A velocidade máxima do carro do meu pai é quantos por cento da velocidade máxima do meu carro?
•  
• 11) Por um descuido meu, perdi R$ 336,00 dos R$ 1.200,00 que eu tinha em meu bolso. Quantos por cento eu perdi desta quantia?
•  
• 12) Dei ao meu irmão 25 das 40 bolinhas de gude que eu possuía. Quantos por cento das minhas bolinhas de gude eu dei a ele? Com quantos por cento eu fiquei?
•  
• 13) Ao comprar um produto que custava R$ 1.500,00 obtive um desconto de 12%. Por quanto acabei pagando o produto? Qual o valor do desconto obtido?
•  
• 14) Na festa de aniversário do meu sobrinho derrubei uma mesa onde estavam 40 garrafas de refrigerante. Sobraram apenas 15% das garrafas sem quebrar. Quantas garrafas sobraram e quantas eu quebrei?
•  
• 15) Dos 28 bombons que estavam na minha gaveta, já comi 75%. Quantos bombons ainda me restam?
•  
• 16) Comprei 30 peças de roupa para revender. Na primeira saída eu estava com sorte e consegui vender 60%. Quantas peças de roupa eu vendi?
•  
• 17) Em uma cesta eu possuía uma certa quantidade de ovos. As galinhas no meu quintal botaram 10% da quantidade dos ovos que eu tinha na cesta e nela os coloquei, mas por um azar meu, um objeto caiu sobre a dita cuja e 10% dos ovos foram quebrados. Eu tenho mais ovos agora ou inicialmente?
•  
• 18) O aumento salarial de uma certa categoria de trabalhadores seria de apenas 6%, mas devido à intervenção do seu sindicato, esta mesma categoria conseguiu mais 120% de aumento sobre o percentual original de 6%. Qual foi o percentual de reajuste conseguido?
•  
• 19) Quanto é 60% de 200% de 80%?
•  
• 20) Quanto é 45% de 90% de 180?
•  
• 21)  Comprei um frango congelado que pesava 2,4kg. Após o descongelamento e de ter escorrido toda a água, o frango passou a pesar apenas 1,44kg. Fui lesado em quantos por cento do peso, por ter levado gelo a preço de frango?
•  
• 22) Em uma população de 250 ratos, temos que 16% são brancos. Qual é o número de ratos brancos desta população?
•  
• 23) Das 20 moedas que possuo em meu bolso, apenas 15% delas são moedas de um real. Quantas moedas de um real eu possuo em meu bolso?
•  
• 24) Dos 8 irmãos que possuo, apenas 12,5% são mulheres. Quantas irmãs eu possuo?
•  
• 25) Tempos atrás o rolo de papel higiênico que possuiu por décadas 40 metros de papel, passou a possuir apenas 30 metros. Como o preço do rolo não sofreu alteração, tal artimanha provocou de fato um aumento de quantos por cento no preço do metro do papel?
•  
• 26) Um guarda-roupa foi comprado a prazo, pagando-se R$ 2.204,00 pelo mesmo. Sabe-se que foi obtido um desconto de 5% sobre o preço de etiqueta. Se a compra tivesse sido à vista, o guarda-roupa teria saído por R$ 1.972,00. Neste caso, qual teria sido o desconto obtido?
•  
•  27) Um jogador de futebol, ao longo de um campeonato, cobrou 75 faltas, transformando em gols 8% dessas faltas. Quantos gols de falta esse jogador fez?
•    
•  28) Se eu comprei uma ação de um clube por R$250,00 e a revendi por R$300,00, qual a taxa percentual de lucro obtida?
• 
  
  
  
   29
  )   Uma grande empresa possui 84 funcionários e sabe-se que cada funcionário fala pelo uma das línguas entre Português e Inglês. Além disso, 20% dos que falam Português também falam Inglês e 80% dos que falam Inglês também falam Português. Quantos funcionários falam as duas línguas?
  
  
  
  
  30) Um grupo de cientistas com Hepatite C foi submetido a um tratamento tradicional em que 40% desses pacientes foram completamente curados.Os pacientes que não obtiveram cura foram distribuídos em dois grupos de mesma quantidade e submetidos a dois tratamentos inovadores. No primeiro tratamento, 35% dos pacientes foram curados e, no segundo, 45%.
  Em relação aos pacientes submetidos inicialmente, os tratamentos inovadores proporcionaram cura de?
  
  
  
  
  31)  Um comerciante revende uma mercadoria por R$ 126,00 com lucro de 40%. Determine o preço de custo dessa mercadoria.
  
  
  32)  Um comerciante aumentou os preços de suas mercadorias em 150%. Como a venda não estava satisfatória, voltou aos preços praticados antes do aumento. Qual foi o percentual de redução em relação aos preços aumentados?
  
  
  33)   O combustível de um carro é composto de 80% de gasolina e 20% de álcool. O litro da gasolina custa R$ 2,00 e o álcool custa R$ 1,20. Se são gastos R$ 101,20 para encher o tanque, qual é a capacidade, em litros, do tanque?
  
  
  34)   Do salário bruto de Paulo, são descontados 15% referentes ao imposto de renda e 12% referentes á assistência médica familiar. Após esses descontos, Paulo recebe o salário de R$ 2190,00. O salário bruto de Paulo é?
  35)  Um lote foi vendido por R$ 20.700,00, com um lucro de 15% sobre o valor inicial; em seguida, revendido por R$ 22.770,00. O lucro total das duas transações, em relação ao valor inicial, equivale a um percentual de?
  
  
  
  
  36)  Uma pesquisa feita entre os alunos do Ensino Fundamental de uma escola revelou que 43% gostam de rock, 11% gostam de rock e de MPB, 59% dos alunos gostam de apenas um dos dois estilos e 60 alunos não gostam de nenhum dos dois estilos. O número de alunos entrevistados foi
  
  
  
  
  37)  Uma mercadoria foi reajustada em 10% e ,em seguida, sofreu um desconto de 10%. Em relação ao preço inicial, esta mercadoria
  
  
  38)                   Em uma cidade há 1200 pessoas que já foram assaltadas de alguma forma, das quais 800 são casadas. Do total de pessoas assaltadas, 60% são mulheres, sendo que 80% são casadas. Quantos são os homens casados que já foram assaltados?
  
  
  39)                   Sobre o preço final do produto de uma fábrica, gastam-se 1/5 com impostos, ¼ com salários, 30% com matéria-prima e o restante é lucro. O percentual do lucro é
  40)                   Uma escada de 12 metros de comprimento está apoiada sob um muro. A base da escada está distante do muro cerca de 8 metros. Determine a altura do muro. 
  
  
  41)                   Do topo de uma torre, três cabos de aço estão ligados à superfície por meio de ganchos, dando sustentabilidade à torre. Sabendo que a medida de cada cabo é de 30 metros e que a distância dos ganchos até à base da torre é de 15 metros, determine a medida de sua altura.
  
  
  41)                   Calcule a metragem de arame utilizado para cercar um terreno triangular com as medidas perpendiculares de 60 e 80 metros, considerando que a cerca de arame terá 4 fios.
  
  
  42)                   Um avião percorreu a distância de 5 000 metros na posição inclinada, e em relação ao solo, percorreu 3 000 metros. Determine a altura do avião.
  
  
  43) Efetue as seguintes transformações:
  a) 6m³ em dm³
  b) 50 cm³ em mm³
  c) 3,632 m³ em mm³
  d) 0,95 dm³ em mm³
  e) 500 dam³ em m³
  f) 8,132 km³ em hm³
  
  
  
  44) Efetue as seguintes transformações:
  a) 2,5 mg em g
  b) 9,56 dg em mg
  c) 0,054 hg em cg
  d) 54 dag em dg
  e) 2,45 kg em hg
  f)2,6 g em kg
  
  
  45) Dê a representação simplificada das seguintes medidas:
  a) doze centímetros cúbicos.
  b) três metros cúbicos e quinze decímetros cúbicos.
  c) seis centímetros cúbicos e doze milímetros cúbicos.
  d) quinze hectômetros cúbicos e cem metros cúbicos.

 

As fatorações são formas diferentes de se representar um mesmo número. Vejamos alguns exemplos:

• Fatorando o número 50 em fatores primos, obtemos a seguinte representação: 2.5²= 50

• Fatorar a expressão x² – 4 consiste em determinar quais expressões algébricas devemos multiplicar para obtê-la. Portanto, veja que (x+2).(x–2) resulta na expressão inicial, ou seja, (x+2).(x–2) é a fatoração de x² – 4;

Na fatoração de números conhecidos, utiliza-se apenas uma maneira: a fatoração em fatores primos. Entretanto, na fatoração algébrica, cada expressão terá um método.

Os métodos de fatoração de expressões algébricas são:

• Fator comum (coloca-se o fator comum em evidência);   
• Agrupamento de fatores comuns;
• Trinômio Quadrado Perfeito;
• Trinômio: x²-Sx+P = 0;
• Diferença de dois quadrados (x²-y²);
• Soma de dois cubos;
• Diferença de dois cubos.

*em vermelho os principais que irão cair na prova.

·         Agrupamento de fatores comuns:

Agrupamento é o método pelo qual simplificamos uma expressão algébrica, agrupando os termos semelhantes (termos em comum).
Ao usarmos o método do agrupamento, necessitamos fazer uso da fatoração: termo comum em evidência.
Observe no exemplo a seguir:

4x² + 8x + 6xy + 12y
Termo comum em evidência em cada agrupamento: 4x² + 8x (8 = 4*2) e 6xy + 12y (12 = 6*2)
4x(x + 2) + 6y(x + 2)
Colocamos novamente em evidência, pois os termos 4x e 6y possuem termos em comum.
(4x + 6y) (x + 2)

Observe mais alguns exemplos de fatoração por agrupamento:

Exemplo 1
2xy – 12x + 3by – 18b
=2x(y – 6) + 3b(y – 6)
=(2x + 3b) (y – 6)

Exemplo 2
6x²b + 42x² – y²b – 7y²
=6x²(b + 7) – y²(b + 7)
=(6x² – y²) (b + 7)

Exemplo 3
x² – 10x + xy – 10y
=x(x – 10) + y(x – 10)
=(x + y) ( x – 10)

Exemplo 4
a³b + a² + 5ab³ + 5b²
=a²(ab + 1) + 5b²(ab + 1)
=(a² + 5b²) (ab + 1)

Exemplo 5
2xy – 4x + 3xy – 6x + 4xy – 8x
=2x(y – 2) + 3x(y – 2) + 4x (y – 2)
=(2x + 3x + 4x) (y – 2)
=9x (y – 2)

.Trinômio do Quadrado Perfeito

Ele só pode ser utilizado quando a expressão algébrica for um trinômio (polinômio com três monômios) e esse trinômio formar um quadrado perfeito.

O que é trinômio

Trinômio é um polinômio que tem três monômios sem termos semelhantes, veja exemplos:

3x² + 2x + 1

20x³ + 5x – 2x²

2ab +5b + 3c

Nem todos os trinômios acima podem ser fatorados utilizando o quadrado perfeito.

Como identificar um trinômio do quadrado perfeito

Para que um trinômio seja quadrado perfeito ele deve ter algumas características:

• Dois termos (monômios) do trinômio devem ser quadrados.
• Um termo (monômio) do trinômio deve ser o dobro das raízes quadradas dos dois outros termos.

Dois membros do trinômio têm raízes quadradas e o dobro delas é o termo do meio, então o trinômio 16x² + 8x + 1 é quadrado perfeito.

Então, a forma fatorada do trinômio é 16x² + 8x + 1 é (4x + 1)², pois é a soma das raízes ao quadrado.

Exemplo 1:

x² +2xy + y²

⁼  (x+y)² -  { porque devemos tirar primeiro as raízes quadradas que são  x² e y². O       dobro dessas raízes deve ser 2 . x . y= 2xy. então esse trinômio é quadrado perfeito.}

.Diferença de dois quadrados:

A fatoração pela diferença de dois quadrados só poderá ser usada quando:

- Tivermos uma expressão algébrica com dois monômios (sejam binômios).
- Os dois monômios sejam quadrados.
- A operação entre eles for de subtração.

As fatorações são formas diferentes de se representar um mesmo número. Vejamos alguns exemplos:

• Fatorando o número 50 em fatores primos, obtemos a seguinte representação: 2.5²= 50

• Fatorar a expressão x² – 4 consiste em determinar quais expressões algébricas devemos multiplicar para obtê-la. Portanto, veja que (x+2).(x–2) resulta na expressão inicial, ou seja, (x+2).(x–2) é a fatoração de x² – 4;

Na fatoração de números conhecidos, utiliza-se apenas uma maneira: a fatoração em fatores primos. Entretanto, na fatoração algébrica, cada expressão terá um método.

Os métodos de fatoração de expressões algébricas são:

• Fator comum (coloca-se o fator comum em evidência);   
• Agrupamento de fatores comuns;
• Trinômio Quadrado Perfeito;
• Trinômio: x²-Sx+P = 0;
• Diferença de dois quadrados (x²-y²);
• Soma de dois cubos;
• Diferença de dois cubos.

*em vermelho os principais que irão cair na prova.

·         Agrupamento de fatores comuns:

Agrupamento é o método pelo qual simplificamos uma expressão algébrica, agrupando os termos semelhantes (termos em comum).
Ao usarmos o método do agrupamento, necessitamos fazer uso da fatoração: termo comum em evidência.
Observe no exemplo a seguir:

4x² + 8x + 6xy + 12y
Termo comum em evidência em cada agrupamento: 4x² + 8x (8 = 4*2) e 6xy + 12y (12 = 6*2)
4x(x + 2) + 6y(x + 2)
Colocamos novamente em evidência, pois os termos 4x e 6y possuem termos em comum.
(4x + 6y) (x + 2)

Observe mais alguns exemplos de fatoração por agrupamento:

Exemplo 1
2xy – 12x + 3by – 18b
=2x(y – 6) + 3b(y – 6)
=(2x + 3b) (y – 6)

Exemplo 2
6x²b + 42x² – y²b – 7y²
=6x²(b + 7) – y²(b + 7)
=(6x² – y²) (b + 7)

Exemplo 3
x² – 10x + xy – 10y
=x(x – 10) + y(x – 10)
=(x + y) ( x – 10)

Exemplo 4
a³b + a² + 5ab³ + 5b²
=a²(ab + 1) + 5b²(ab + 1)
=(a² + 5b²) (ab + 1)

Exemplo 5
2xy – 4x + 3xy – 6x + 4xy – 8x
=2x(y – 2) + 3x(y – 2) + 4x (y – 2)
=(2x + 3x + 4x) (y – 2)
=9x (y – 2)

.Trinômio do Quadrado Perfeito

Ele só pode ser utilizado quando a expressão algébrica for um trinômio (polinômio com três monômios) e esse trinômio formar um quadrado perfeito.

O que é trinômio

Trinômio é um polinômio que tem três monômios sem termos semelhantes, veja exemplos:

3x² + 2x + 1

20x³ + 5x – 2x²

2ab +5b + 3c

Nem todos os trinômios acima podem ser fatorados utilizando o quadrado perfeito.

Como identificar um trinômio do quadrado perfeito

Para que um trinômio seja quadrado perfeito ele deve ter algumas características:

• Dois termos (monômios) do trinômio devem ser quadrados.
• Um termo (monômio) do trinômio deve ser o dobro das raízes quadradas dos dois outros termos.

Dois membros do trinômio têm raízes quadradas e o dobro delas é o termo do meio, então o trinômio 16x² + 8x + 1 é quadrado perfeito.

Então, a forma fatorada do trinômio é 16x² + 8x + 1 é (4x + 1)², pois é a soma das raízes ao quadrado.

Exemplo 1:

x² +2xy + y²

⁼  (x+y)² -  { porque devemos tirar primeiro as raízes quadradas que são  x² e y². O       dobro dessas raízes deve ser 2 . x . y= 2xy. então esse trinômio é quadrado perfeito.}

.Diferença de dois quadrados:

A fatoração pela diferença de dois quadrados só poderá ser usada quando:

- Tivermos uma expressão algébrica com dois monômios (sejam binômios).
- Os dois monômios sejam quadrados.
- A operação entre eles for de subtração

.►Como escrever a forma fatorada dessas expressões algébricas. 

Dada a expressão algébrica 16x² – 25, veja os passos que devemos tomar para chegarmos a forma fatorada utilizando o 5º caso de fatoração. 

A forma fatorada será (4x – 5) (4x + 5).